3- Teoremas de Redes
- Introducción
- Teorema de Superposición
- Teorema de Thévenin
- Teorema de Norton
- Teorema de Máxima Transferencia de Potencia
- Teorema de Sustitución
- Teorema de Reciprocidad
1. Introducción
Para analizar cualquier tipo de circuito (o red) basta con emplear las leyes de Ohm y las de Kirchhoff. Pero también es cierto que, basados en estas leyes, se pueden derivar ciertos teoremas. Los teoremas consisten en reglas relativamente simples o "atajos" que facilitan la resolución de problemas y además permiten aislar efectos, encontrar equivalencias, etc.
Observación:
- Los teoremas que se van a analizar sólo se
pueden aplicar a circuitos lineales y bilaterales.
- circuito lineal: cuando las características (o comportamiento) de sus elementos son independientes del voltaje aplicado y de la corriente que circula por ellos. Ejemplo: un circuito compuesto por resistores es lineal porque los valores de las resistencias son independientes del V y la I. Asimismo, un circuito no será lineal si, por ejemplo, contiene al menos un VDR.
- circuito bilateral: cuando las características (o comportamiento) de sus elementos son independientes de la polaridad aplicada. El diodo (que se estudiará en la asignatura "Circuitos Electrónicos I"), constituye un ejemplo de elemento cuyas características no son independientes de la polaridad aplicada.
Arriba
2.Teorema de Superposición
En un circuito con múltiples fuentes, la corriente o el voltaje en cualquier punto puede calcularse como la suma algebraica de las contribuciones individuales de cada fuente al actuar sola.
Procedimiento: para aislar una fuente se anulan los efectos de las demás. Es decir:
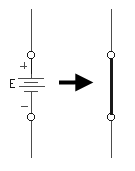
- las fuentes independientes de voltaje se sustituyen por cortocircuitos (E=0),
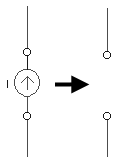
- las fuentes independientes de corriente se sustituyen por circuitos abiertos (I=0),
- ídem para las fuentes dependientes, sólo si la variable de control no es parte del circuito sobre el que se está aplicando el teorema. Es decir, no se pueden pasivar las fuentes dependientes cuya variable de control se encuentra en el mismo circuito que la fuente.
Observaciones:
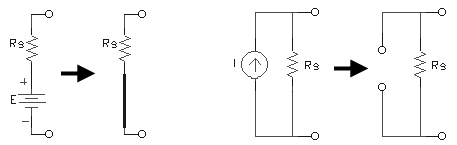
- Si se encuentran presentes fuentes prácticas (no ideales), cuando se eliminan dichas fuentes, se debe seguir considerando el efecto de sus resistencias internas.
- Es posible considerar los efectos de más de una fuente a la vez.
- Este principio puede aplicarse a cualquier efecto relacionado linealmente con su causa, por lo tanto no se aplica a funciones no lineales tales como la potencia.
- Aplicar este principio presenta varias ventajas:
- Se subdivide el problema en otros más sencillos y de menor complejidad matemática.
- Permite conocer la contribución de cada fuente a la magnitud bajo investigación.
- La aplicación más usual de este teorema es en circuitos donde se realiza el análisis de DC y AC por separado y luego se suman para obtener la solución total.
Arriba
3. Teorema de Thévenin
Un circuito de CD de dos terminales formado por resistores y fuentes independientes y/o dependientes, puede reemplazarse por un circuito equivalente consistente en una fuente de voltaje (ETH) con un resistor en serie (RTH).
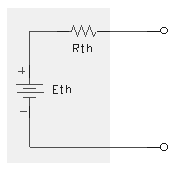
Como se observa en la figura,
- el valor de ETH se puede determinar midiendo o calculando el voltaje de circuito abierto entre terminales
- el valor de RTH se puede obtener midiendo o calculando la corriente de corto circuito para determinar RTH= ETH / Isc
Entonces, dado un determinado circuito, se puede determinar su equivalente Thévenin de la siguiente manera:
Procedimiento:
- Se señalan los terminales del circuito a reemplazar por su equivalente Thévenin.
- Para obtener ETH se calcula el voltaje de circuito abierto (Voc) entre las terminales marcadas.
- Para obtener RTH se determina el tipo de circuito a reemplazar:
-- Si el circuito contiene sólo fuentes independientes, se pasivan todas las fuentes y se determina la resistencia equivalente entre terminales.
-- Si el circuito contiene fuentes dependientes e independientes, para calcular RTH primero se debe encontrar el voltaje de circuito abierto entre terminales y luego la corriente de cortocircuito. Así: RTH = Voc / Isc .
-- Si se trata de una red que sólo contiene fuentes dependientes, su equivalente es RTH. Un método para determinar RTH consiste en colocar entre terminales una fuente ficticia de voltaje (o corriente) y calcular la corriente (o voltaje) entre terminales. Así: RTH = voltaje de la fuente / corriente calculada (o voltaje calculado / corriente de la fuente).
Procedimiento experimental:
- Para obtener ETH se mide con un voltímetro el voltaje de circuito abierto entre los terminales marcados.
- Para obtener RTH existen dos opciones:
-- se mide la corriente de cortocircuito para calcular la resistencia equivalente entre terminales como Voc / Isc.
-- se coloca un resistor variable entre los terminales marcados ajustando su valor hasta que el voltímetro midiendo entre sus extremos indique ETH/2. En ese momento el valor del resistor variable=RTH.
Observaciones:
- No se debe separar la fuente dependiente de su variable de control cuando se determinan los terminales.
- La RTH se puede obtener a través del análisis Transfer Function del software de simulación PSpice, donde RTH=Rout.
Arriba
4. Teorema de Norton
Un circuito de CD de dos terminales formado por resistores y fuentes independientes y/o dependientes, puede reemplazarse por un circuito equivalente consistente en una fuente de corriente (IN) con un resistor en paralelo (RN).
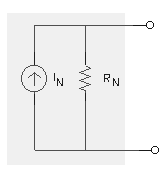
Procedimiento:
- Se señalan los terminales del circuito a reemplazar por su equivalente Norton.
- Para obtener IN se calcula la corriente de cortocircuito entre las terminales marcadas.
- Como RN = RTH , para obtener RN se procede de la manera analizada al estudiar el equivalente Thévenin.
Observaciones:
- Ídem Teorema de Thévenin.
- La transformación de fuentes (TP Nº 2) equivale a convertir un circuito equivalente Thévenin en un circuito equivalente Norton o viceversa.
Arriba
5. Teorema de la Máxima Transferencia de Potencia
Un circuito de CD entregará su máxima potencia a la carga (RL) cuando RL=RTH .
Demostrado con Mathematica:

Ejemplo numérico:
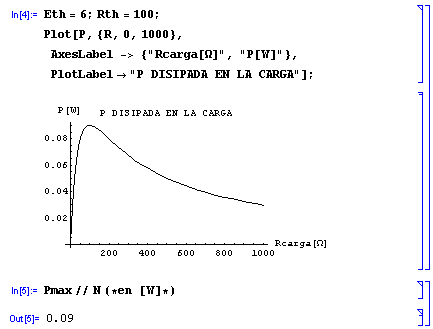
Empleando una escala semilogarítmica:
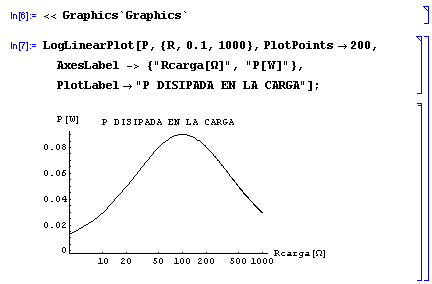
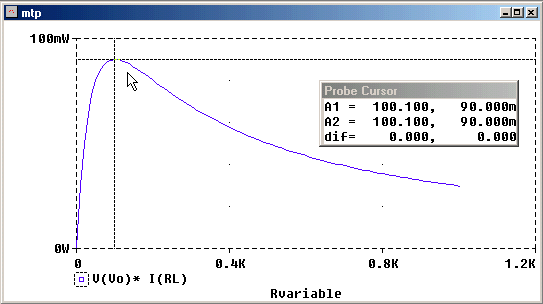
El mismo ejemplo en PSpice:
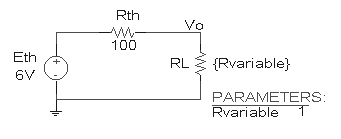
En Schematics, la resistencia de carga se define variable. En PSpice AD, graficamos la potencia (=V.I) en función del parámetro variable.
Arriba
6. Teorema de Sustitución
Si en un circuito de CD, se conocen el voltaje y la corriente que pasan por cualquier rama, ésta puede sustituirse con otra rama que mantenga los mismos niveles de voltaje y corriente.
Ejemplo:
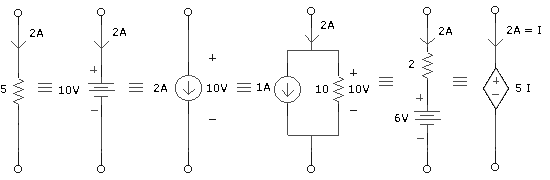
Observaciones:
- Sustituir V=0 por un cortocircuito o I=0 por un circuito abierto, consiste en una aplicación particular del Teorema de Sustitución.
- Cuando se conoce la diferencia de voltaje en una rama, los elementos de esa sección del circuito pueden sustituirse por una fuente de tensión. Esto permite aislar una parte de la red y trabajar con ella como si se tratara de un circuito independiente.
Ejemplo:
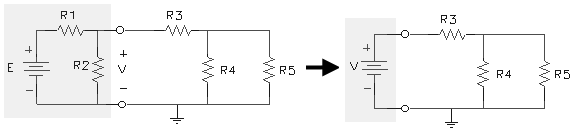
Arriba
7. Teorema de Reciprocidad
La corriente I en cualquier rama de un circuito, debida a una única fuente de voltaje ubicada en otra parte del circuito, será igual a la corriente que pasa por la rama en la cual se ubicaba originalmente la fuente si ésta se coloca en la rama en la cual se midió originalmente la corriente I.
Observaciones:
- Este teorema se aplica sólo a redes de fuente única.
Ejemplo:
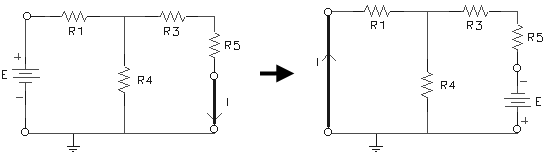
Arriba
Teoría de Circuitos I - Última modificación: Mayo 28, 2002