9- Potencia de CA en Estado Estable
- ¿Cómo se obtiene la potencia instantánea?
- ¿Qué es la potencia activa (P)?
- ¿Qué es la potencia reactiva (Q)?
- ¿En qué consisten el factor de potencia (fp) y el factor de potencia reactiva (fr)?
- ¿Qué es la potencia aparente (S)?
- ¿Qué es el triángulo de potencia?
- ¿Cómo se realiza el análisis de potencia en circuitos serie, paralelo o mixtos?
- ¿Cómo se obtiene la Máxima Transferencia de Potencia?
- ¿Cómo se mejora el factor de potencia?
1. ¿Cómo se obtiene la potencia instantánea?
Si v(t) e i(t) son señales sinusoidales, entonces la potencia en cualquier instante se define como:
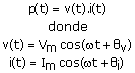
Al trabajar en estado estacionario podemos elegir cualquier referencia para el tiempo cero. Los ingenieros han encontrado conveniente usar como tiempo cero el que corresponde al instante en que la corriente pasa por un máximo positivo. Esto implica un desplazamiento de los ángulos de fase del voltaje y la corriente:
![]()
Sustituyendo estas ecuaciones, encontramos que la expresión de la potencia instantánea es:
![]()
Por medio del empleo de identidades trigonométricas, se obtiene:
![]()
Se puede apreciar que la frecuencia de la potencia instantánea es dos veces la frecuencia del voltaje (o de la corriente).
Arriba
2. ¿Qué es la potencia activa (P)?
La potencia media, activa o real, es decir la potencia transformada de forma eléctrica en no eléctrica, es el promedio de la potencia instantánea a lo largo de un periodo.
![]()
si primero desarrollamos p(t), se obtiene:
![]()
El valor medio se debe al primer término, porque la integral de cos 2wt y de sen 2wt es cero para un periodo. Entonces:
![]()
Su unidad es el Watt [W].
Ejemplo 1:
En el caso de una red puramente resistiva, la energía eléctrica se transforma totalmente en energía térmica.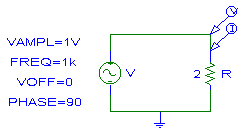
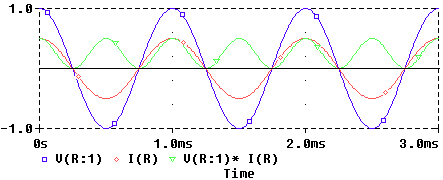
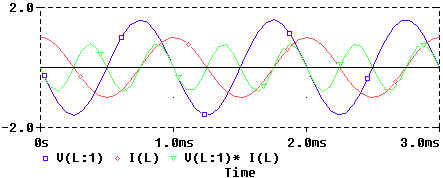
En el caso de un circuito puramente inductivo, la corriente se encuentra retrasada exactamente 90º con respecto al voltaje (es decir qi=qv-90º) y como qv-qi=90º Þ P es cero. En una red de estas características, la energía oscila entre el circuito y la fuente que lo alimenta. Es decir, cuando la potencia instantánea, p(t), es positiva se almacena energía en los campos magnéticos de los elementos inductivos, y cuando es negativa se extrae.
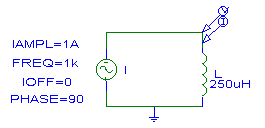
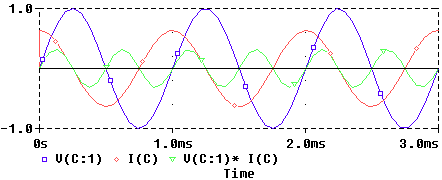
En el caso de un circuito puramente capacitivo, la corriente se encuentra adelantada exactamente 90º con respecto al voltaje (es decir qi=qv+90º) y como qv-qi= -90º Þ P es cero. En una red de estas características, la energía también oscila entre el circuito y la fuente que lo alimenta. Es decir, cuando p(t) es positiva se almacena energía en los campos eléctricos de los elementos capacitivos, y cuando es negativa se extrae.
Arriba
3. ¿Qué es la potencia reactiva (Q)?
Es la potencia asociada a un circuito puramente inductivo o capacitivo. Esta potencia oscila entre los elementos reactivos (inductores y capacitores) y el resto del circuito (como dijimos antes: se acumula en el campo magnético en el inductor y en el campo eléctrico en el capacitor y luego es devuelta al sistema).
Su expresión es:
![]()
Observaciones:
-
Para diferenciarla de la potencia activa, la unidad de la potencia reactiva es el [VAR], que surge como acrónimo de volt-ampere reactivo.
-
Para inductores Q es positiva, porque qv-qi=90º y sen(qv-qi) = 1.
- Para capacitores Q es negativa, porque qv-qi= -90º y sen(qv-qi) = -1.
-
En términos de P y Q, la potencia instantánea es:
![]()
Arriba
4. ¿En qué consisten el factor de potencia (fp) y el factor de potencia reactiva (fr)?
El ángulo qv- qi = j se conoce como ángulo del factor de potencia. Así, se definen:
factor de potencia = fp = cos (qv-qi) = cosj
factor de potencia reactiva = fr = sen (qv-qi) = senj
Observaciones:
- como cosj = cos -j , para describir completamente al factor de potencia, se emplea una de las siguientes frases: "en retraso" o "en adelanto".
- el factor de potencia en retraso implica que la corriente está retrasada con respecto al voltaje, entonces la carga es inductiva y j >0.
- el factor de potencia en adelanto implica que la corriente está adelantada con respecto al voltaje, entonces la carga es capacitiva y j <0.
- en un circuito puramente capacitivo o inductivo el fp=0 y fr=1.
- en un circuito puramente resistivo el fp=1 y fr=0.
Arriba
5. ¿Qué es la potencia aparente (S)?
Se define a la potencia compleja como la suma compleja de la potencia activa y la potencia reactiva:
S = P + jQ
Donde la magnitud de la potencia compleja ½S½ se denomina potencia aparente.
Como P=Vef Ief cos (qv-qi) y Q=Vef Ief sen (qv-qi), entonces:
![]()
Analizando la última ecuación, vemos también se puede expresar la potencia compleja, en función del fasor de voltaje y del fasor conjugado de la corriente:
![]()
Hay dos variantes de esta ecuación:
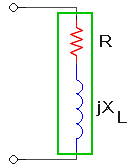
1º) sustituyendo el voltaje:
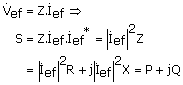
donde X es la reactancia equivalente del circuito (positiva para circuitos inductivos y negativa para circuitos capacitivos).
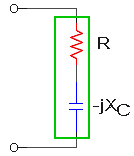
2º) sustituyendo la corriente:
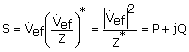
Observaciones:
-
Si bien la potencia aparente tiene las mismas dimensiones que la potencia activa y la reactiva, para diferenciarla, como unidad se utiliza el [VA] (acrónimo de volt-ampere).
-
Ief* es el conjugado de la corriente y Z* es el conjugado de la impedancia.
Arriba
6. ¿Qué es el triángulo de potencia?
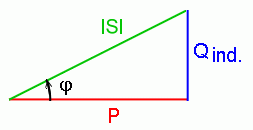
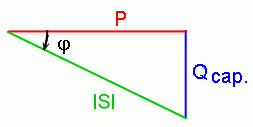
|S|, P y Q pueden representarse geométricamente mediante un triángulo rectángulo, éste precisamente es el triángulo de potencia. Donde el ángulo que forman P y |S| es el ángulo (j) del fp.
 |
 |
 |
 |
Observación:
- Si una red tiene tanto elementos capacitivos como inductivos, el componente reactivo del triángulo de potencia se determinará mediante la diferencia entre la potencia reactiva proporcionada a cada uno. Si QL > QC el triángulo de potencia resultará semejante a un diagrama de potencia con características inductivas. En caso contrario será semejante a un diagrama de potencias con características capacitivas.
Arriba
7. ¿Cómo se realiza el análisis de potencia en circuitos serie, paralelo o mixtos?
Las potencias totales P, Q y S pueden calcularse, independientemente de la configuración del circuito, como la suma de las potencias en cada rama de la red bajo análisis.
Lo anterior no es válido para la potencia aparente. La potencia aparente total |St| puede obtenerse aplicando el teorema de Pitágoras una vez encontradas Pt y Qt.
Ejemplo 4:
Obtener la información de potencia para cada elemento del siguiente circuito y construir el triángulo de potencia. (I=14.14 Ð 30º. La corriente efectiva es 14.14/Ö 2 = 10 A)
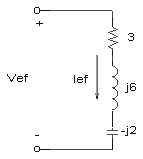
| 1º forma) se analiza cada elemento por separado | 2º forma) primero se obtiene la impedancia equivalente |
|
P=(10)2.3 = 300W Qj6=(10)2.6 = 600 VARind Q-j2=(10)2.2 = 200 VARcap |S|=Ö [(300)2+(600-200)2] = 500 VA fp=P/S = 0.6 atrasado |
Zeq=R+j(XL-XC)=3+j4 P=(10)2.3 = 300W Qj4W=(10)2.4 = 400 VARind |S|=Ö [(300)2+(400)2] = 500 VA fp=P/S = 0.6 atrasado |
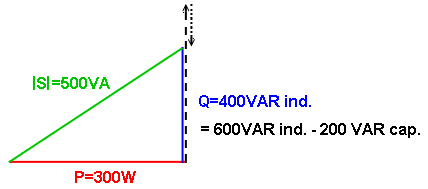
Ejemplo 5:
Tomemos una red con tres ramas en paralelo;
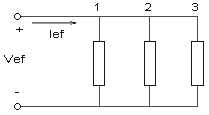
donde las cargas 1 y 3 tienen características inductivas y la carga 2 capacitiva. El triángulo de potencia total para el circuito se puede obtener uniendo los vértices de los triángulos de potencia para cada rama:
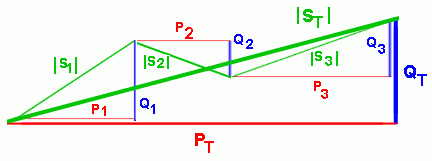
Arriba
8. ¿Cómo se obtiene la Máxima Transferencia de Potencia?
Hay ocasiones en las cuales la eficiencia puede ser un aspecto secundario y lo que interesa es transmitir la mayor cantidad posible de potencia a la carga (por ejemplo, transmisión de información a través de señales eléctricas).
La máxima transferencia de potencia media a la carga, en el caso de una red que funciona en estado estacionario sinusoidal, se obtiene cuando la carga presenta una impedancia igual a la conjugada de la impedancia equivalente de Thévenin vista desde los terminales de la carga.
Es decir que dada una red lineal que funciona en estado estacionario sinusoidal, ésta se puede reemplazar por su equivalente Thévenin, y la corriente eficaz que circula por la carga será:
![]()
(suponiendo que VTh se expresa como valor eficaz). La potencia media suministrada a la carga será:
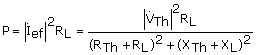
Para maximizar la potencia, ¶P/RL y ¶P/XL deberán ser nulas. De estas condiciones se obtiene que:
![]()
Combinando ambas expresiones se demuestra que la condición para MTP es ZL=ZTh*
En Mathematica:
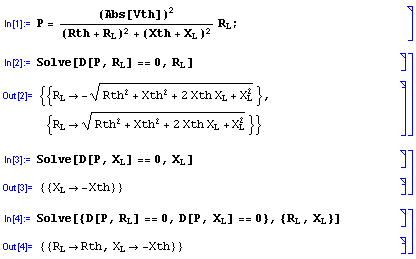
Observación:
-
Puede ocurrir que los valores de RL y XL se encuentren restrigidos a un cierto intervalo. En ese caso, se procede a ajustar primero XL al valor más próximo de -XTh y luego se procede a ajustar RL al valor más próximo al óptimo.
Arriba
9. ¿Cómo se mejora el factor de potencia?
Mejorar el factor de potencia de una red, consiste en acercar su valor a la unidad. De esta manera, a igual potencia activa, se reduce la corriente que circula por la red. Finalidades:
- disminuir las pérdidas de energía,
- disminuir la sección de los conductores de las líneas de transporte y distribución,
- facilitar la regulación de la tensión,
- evitar recargos en la facturación de energía eléctrica.
Para ello se debe reducir la componente reactiva del triángulo de potencia. Como las cargas en la industria son mayormente inductivas, se conectan en paralelo "bancos de capacitores" lo más cerca posible del lugar de consumo. Con esto se evita la circulación de gran parte de la corriente desde la central eléctrica.
Observaciones:
- Analizar los ejemplos 19.5 y 19.6 presentados por Boylestad.
- El análisis de este tema se profundiza en la asignatura: "Máquinas e Instalaciones Eléctricas".
Arriba
Teoría de Circuitos I - Última modificación: Mayo 28, 2002