1. ¿A qué se denomina red de dos puertos?
2. ¿Cómo se modelan las redes de dos puertos?
3. ¿Cómo se determinan los distintos parámetros?
4. Conversión de parámetros
5. ¿Cómo se analizan los circuitos de dos puertos cargados?
6. Interconexión de circuitos de dos puertos

Tablas (conversión de parámetros y ecuaciones para cuadripolos cargados)

1. ¿A qué se denomina red de dos puertos?

Primero aclaremos que un puerto (o puerta) es un par de terminales donde se verifica que la corriente que ingresa por un terminal es igual a la corriente que sale por el otro.  Si un circuito presenta dos pares de terminales se lo denomina red de dos puertos o cuadripolo.

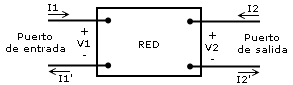
En la figura I1=I1' e I2=I2' (condición de puerto).

Centraremos nuestro estudio en las redes de dos puertos que cumplan las siguientes condiciones:

• que no contengan energía almacenada, es decir con condiciones iniciales nulas;
• que tampoco contengan fuentes independientes; y
• donde los puertos no se interconecten externamente 

Observación:

• Los cuadripolos son de gran utilidad para simplificar el análisis de circuitos.  Cuando no interesan los valores de las variables internas, el circuito puede considerarse como una "caja negra" y por consiguiente ser modelado con apenas dos ecuaciones simultáneas.

Arriba

2. ¿Cómo se modelan las redes de dos puertos?

Cuando se trabaja con cuadripolos, interesa relacionar las variables terminales V1, V2, I1 e I2.  Dos de las cuatro variables son independientes, por lo que el cuadripolo se puede modelar con un sistema de dos ecuaciones.

Así, es posible formar seis sistemas de ecuaciones:

• (V1,V2) = f (I1,I2) y su inversa (I1,I2) = f (V1,V2)
• (V1,I1) = f (V2,I2) y su inversa (V2,I2) = f (V1,I1)
• (V1,I2) = f (V2,I1) y su inversa (V2,I1) = f (V1,I2)

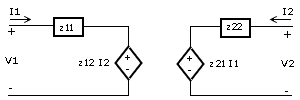
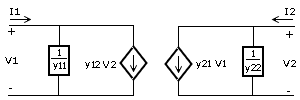
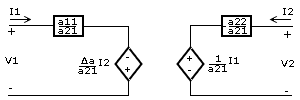
Sistema de ecuaciones	En forma matricial	Circuito equivalente

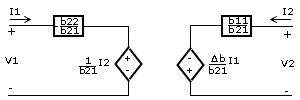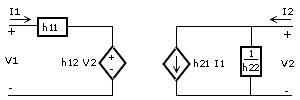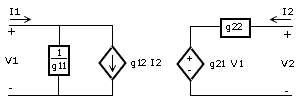Los coeficientes presentes en las ecuaciones se conocen como parámetros del cuadripolo.

Arriba

3. ¿Cómo se determinan los distintos parámetros?

Los parámetros se pueden calcular o medir anulando una de las variables independientes.  Por ejemplo para determinar los valores de los parámetros z, primero se anula I2 (condición de circuito abierto de salida) y se obtiene:

Luego se restaura I2 y se anula I1 (condición de circuito abierto de entrada) y se obtiene:

Se observa que los parámetros z se expresan en ohms.  Por esto reciben el nombre de parámetros impedancia.

Análogamente, se pueden obtener los parámetros:

• y = parámetros admitancia
• a = parámetros transmisión o parámetros ABCD
• b = parámetros transmisión inversa
• h = parámetros híbridos (empleados en el análisis de circuitos con transistores)
• g = parámetros híbridos inversos

Ejemplo:

Resolución del ejercicio n°3 del trabajo práctico n°12:

Observación:

• Existen casos especiales que permiten simplificar la cantidad de cálculos a realizar para determinar un conjunto de parámetros:
  • los circuitos recíprocos requieren sólo de tres cálculos o mediciones
  • los circuitos simétricos requieren sólo de dos cálculos o mediciones

Arriba

4. Conversión de parámetros

Como todos los conjuntos de parámetros dependen de las mismas variables, dado un conjunto de parámetros conocido se pueden determinar los cinco conjuntos restantes.

Se puede demostrar que:

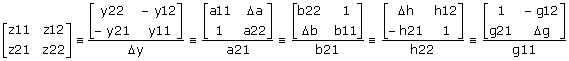
La primera equivalencia se obtiene planteando el sistema de ecuaciones basado en parámetros admitancia y despejando (V1,V2) = f (I1,I2).  Por comparación con el sistema de ecuaciones basado en parámetros impedancia se encuentra la equivalencia entre coeficientes.

En Mathematica:

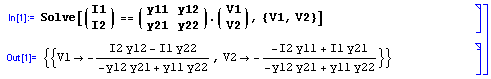
Se trabaja de forma análoga para encontrar las equivalencias restantes.

Arriba

5. ¿Cómo se analizan los circuitos de dos puertos cargados?

Dado un cuadripolo, que es alimentado a través del puerto de entrada y cargado a la  salida, como se muestra en la figura:

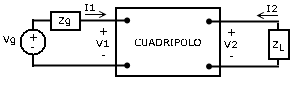
donde:

• Vg: voltaje de la fuente ideal

• Zg: impedancia interna del generador

• Z_L: impedancia de la carga

cualquier característica del circuito que defina su comportamiento terminal puede ser calculada a partir del siguiente sistema de ecuaciones:

• V1 = Vg - I1 Zg

• V2 = - I2 ZL

• + sistema de ecuaciones que modela al cuadripolo

Generalmente interesa conocer:

• impedancia de entrada Zin=V1/I1

• corriente I2

• equivalente Thévenin con respecto al puerto 2

• ganancia de corriente I2/I1

• ganancia de voltaje V2/V1

• ganancia de voltaje V2/Vg

Arriba

6. Interconexión de circuitos de dos puertos

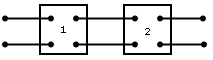
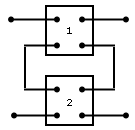
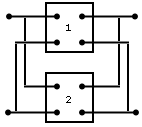
cascada	serie		paralelo
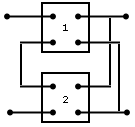
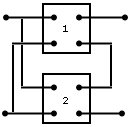
serie-paralelo		paralelo-serie

Dado un par de cuadripolos conectados en ...

... cascada, el producto de sus matrices de transmisión da como resultado la matriz de transmisión general.

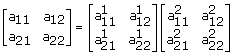
... serie, la suma de sus matrices de impedancia da como resultado la matriz de impedancia general.

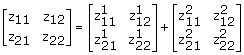
... paralelo, la suma de sus matrices de admitancia da como resultado la matriz de admitancia general.

Arriba

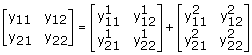
Teoría de Circuitos I - Última modificación: Mayo 28, 2002