1- Introducción - Circuitos Resistivos
- Algunas definiciones
- ¿Qué sistema de unidades utilizamos?
- ¿Qué convención de signos utilizamos para corriente y voltaje?
- ¿Qué representa obtener un valor negativo de corriente? (ídem voltaje)
- ¿Cuál es la notación para indicar voltaje?
- ¿Qué establece la Ley de Ohm?
- ¿Qué es un cortocircuito?¿Y un circuito abierto?
- ¿Qué convención de signos utilizamos para la potencia?
- ¿Cómo se resuelven los circuitos resistivos?
- ¿En qué consiste la transformación D-Y?
- ¿Qué plantean las Leyes de Kirchhoff?
- ¿Cómo se resuelven los circuitos con fuentes múltiples en serie o paralelo?
- ¿En qué consiste el "análisis de la corriente de rama"?
- ¿En qué consiste la técnica de "reducir y regresar"?
- ¿Cómo se obtiene la expresión del divisor de corriente ?
- ¿Cómo se obtiene la expresión del divisor de tensión?
- ¿A qué se denominan puentes de medida?
1. Algunas definiciones
Nodo: unión de dos o más elementos.
Nodo esencial: unión de más de dos elementos.
Rama: trayectoria comprendida entre dos nodos (=elemento o combinación de elementos en serie comprendidos entre dos nodos).
Rama esencial: trayectoria comprendida entre dos nodos esenciales.
Lazo: trayectoria cerrada (=el nodo de partida coincide con el nodo de llegada).
Malla o ventana: trayectoria cerrada que no contiene a otro lazo.
Circuito planar o plano: circuito que puede dibujarse en una superficie plana, sin que ninguna rama pase sobre otra.
2. ¿Qué sistema de unidades utilizamos?
Sistema Internacional de Unidades.
Unidades SI básicas
| Cantidad | Nombre | Símbolo |
| Longitud | metro | m |
| Masa | kilogramo | kg |
| Tiempo | segundo | s |
| Corriente eléctrica | amper | A |
| Temperatura | kelvin | K |
| Cantidad de sustancia | mol | mol |
| Intensidad luminosa | candela | cd |
Unidades SI derivadas con nombres especiales
| Cantidad | Nombre | Símbolo | En términos de otras unidades |
|
Frecuencia |
hertz |
Hz |
|
|
Fuerza |
newton |
N |
m . kg / s2 |
|
Presión, esfuerzo, tensión |
pascal |
P |
N / m2 |
|
Energía, trabajo, cantidad de calor |
joule |
J |
N.m |
|
Energía, flujo radiante |
watt |
W |
J / s |
|
Carga eléctrica, cantidad de electricidad |
coulomb |
C |
J / V = A.s |
|
Potencial eléctrico, diferencia de potencial, fuerza electromotriz |
volt |
V |
W / A |
|
Capacitancia |
farad |
F |
C / V = A.s/V |
|
Resistencia eléctrica |
ohm |
W |
V / A |
|
Conductancia eléctrica |
siemens |
S |
A / V |
|
Flujo magnético |
weber |
Wb |
V.s |
|
Densidad de flujo magnético |
tesla |
T |
Wb/ m2 |
|
Inductancia |
henry |
H |
Wb/A = V.s/A |
|
Temperatura Celsius |
grado Celsius |
ºC |
|
|
Flujo lumínico |
lumen |
lm |
|
|
Emitancia luminosa (iluminancia) |
lux |
lx |
Im / m2 |
No olvidar indicar las magnitudes con el prefijo adecuado:
| 10-18 | 10-15 | 10-12 | 10-9 | 10-6 | 10-3 | 1 | 103 | 106 | 109 | 1012 |
|
a atto |
f femto |
p pico |
n nano |
µ micro |
m mili |
|
k kilo |
M mega |
G giga |
T tera |
Arriba
3. ¿Qué convención de signos utilizamos para corriente y voltaje?
Para un elemento resistivo aislado, la polaridad de la caída de voltaje se indica en la siguiente figura:
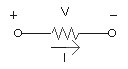
Una inversión de la corriente invertirá la polaridad, es decir:
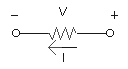
En general, el sentido de la corriente se establece desde el voltaje más alto (+) al más bajo (-). Esta convención se denomina convención de signos pasiva.
Arriba
4. ¿Qué representa obtener un valor negativo de corriente? (ídem voltaje)?
Obtener un valor negativo (al realizar un cálculo) indica que el sentido real es inverso al supuesto.
Arriba
5. ¿Cuál es la notación para indicar voltaje?
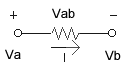
5.1 Notación de subíndice único Va , Vb : especifica el voltaje en el punto a con respecto a tierra o masa (0 volts)
5.2 Notación de doble subíndice Vab : especifica la diferencia de voltaje entre los puntos a y b. Es decir Vab = Va - Vb
Arriba
6. ¿Qué establece la Ley de Ohm?
La ley de Ohm establece que el voltaje a través de una resistencia es directamente proporcional a la corriente que fluye a través de la misma. Es decir:
V ~ I Þ V = R . I
donde R es una constante de proporcionalidad denominada resistencia. Su unidad es:
[V/A] = [W] ohm
A su vez, se define a la conductancia como:
G = 1/R = [1/W] = [S] siemens
Ley de Ohm graficada con Mathematica:
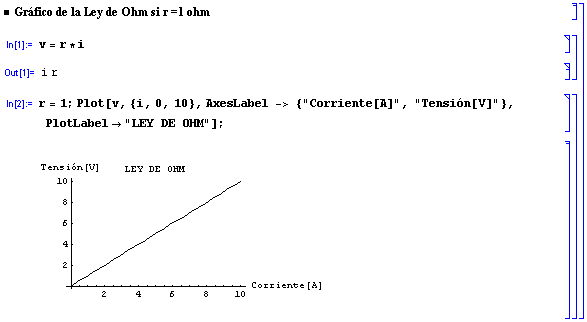
Aprovechamos para analizar otras opciones del software:
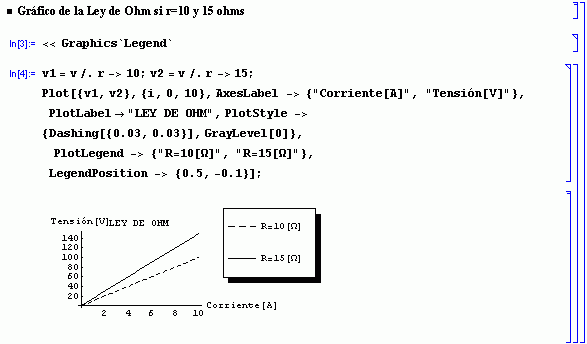
Arriba
7. ¿Qué es un cortocircuito?¿Y un circuito abierto?
Consideremos el siguiente circuito:
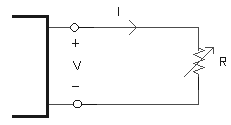
Si R = 0 Þ el resistor se reemplaza por un cortocircuito:
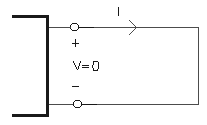
Un cortocircuito es una conexión directa de muy baja resistencia entre dos terminales de un circuito. Puede conducir corriente de un nivel determinado, pero la diferencia de potencial entre sus extremos es cero.
En cambio, si R ® ¥ Þ el resistor se reemplaza por un circuito abierto:
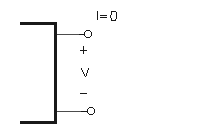
Un circuito abierto consiste simplemente en dos terminales aislados entre sí. Puede haber una diferencia de potencial entre dichos terminales, pero no circula corriente alguna.
Bibliografía: para mayores detalles consultar:
- Boylestad - "Análisis Introductorio de Circuitos" - 8va edición - sección 6-8 (Los circuitos abiertos y los cortocircuitos).
Arriba
8. ¿Qué convención de signos utilizamos para la potencia?
P = P.V = I2 .R = V2 / R
La potencia se genera (=proporciona, entrega, cede, suministra) o absorbe (=disipa, consume) dependiendo de la polaridad del voltaje y de la dirección de la corriente.
8.1 La potencia es generada por un elemento si la corriente "entra por el terminal negativo (o de menor voltaje)" o "sale por el terminal positivo (o de mayor voltaje)". Su valor es negativo.
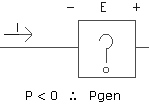
8.2 La potencia es absorbida por un elemento si la corriente "entra por el terminal positivo (o de mayor voltaje)" o "sale por el terminal negativo (o de menor voltaje)". Su valor es positivo.
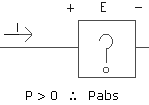
Observaciones:
-
una fuente puede absorber o consumir potencia en el caso de circuitos con múltiples fuentes.
-
en los elementos resistivos, toda la potencia recibida se disipa en forma de calor. Como la polaridad del voltaje se define mediante la dirección de la corriente (y viceversa) y como la corriente siempre se introduce por el terminal positivo, en estos elementos la potencia es siempre positiva.
Ejemplo 1:
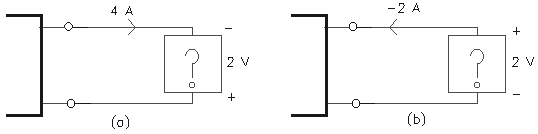
P(a) = V. I = 2 [V]. (-4 [A]) = - 8 [W] ; la corriente tiene signo negativo (según la convención para ser positiva tiene que circular desde el punto de mayor potencial al de menor). Como la potencia es negativa, implica que el elemento está generando potencia. Otra manera de obtener lo mismo: vemos que la corriente ingresa al terminal negativo del elemento, por lo tanto se trata de potencia negativa o generada.
P(b) = V. I = 2 [V]. 2 [A] = 4 [W] ; la corriente tiene signo positivo (porque circula desde el punto de mayor al de menor potencial). Por lo tanto la potencia es positiva, o absorbida; es decir que el elemento está consumiendo potencia.
En síntesis, la manera de expresar los resultados es la siguiente:
1ºcaso: P = - 8 [W] (generada)
2ºcaso: P = 4 [W] (absorbida)
Arriba
9. ¿Cómo se resuelven los circuitos resistivos?
El método a seguir depende de las características del circuito y de los datos e incógnitas.
9.1 Para los elementos en serie, la resistencia total es igual a la suma de las resistencias individuales.
9.2 Para los elementos en paralelo, la conductancia total es igual a la suma de las conductancias individuales.
Observación: como la resistencia equivalente de elementos en paralelo es menor que el valor del menor de los elementos involucrados, si entre estos elementos se encuentra una resistencia muy baja o nula (¡cortocircuito!) el resto del circuito "ve" una resistencia equivalente nula. Se dice que los elementos están cortocircuitados y no circula corriente por ellos (toda la corriente se deriva por el cortocircuito porque es la trayectoria que presenta menor resistencia a su paso).
9.3 Para los elementos en configuración D (delta, o triángulo, o pi), o configuración Y (o estrella, o T) se hace uso de la transformación D-Y.
9.4 Si el circuito presenta múltiples fuentes en serie o paralelo, primero se encuentra su equivalente.
9.5 Si el circuito presenta múltiples resistores y fuentes en configuraciones complicadas se emplea el "análisis de la corriente de rama".
9.6 Para los elementos serie-paralelo (por ejemplo: redes escalera) se puede emplear la técnica de "reducir y regresar".
Arriba
10. ¿En qué consiste la transformación D-Y?
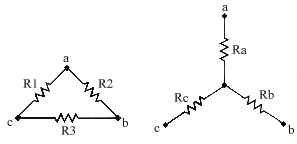
Como la configuración D es equivalente a la configuración Y, se puede demostrar que:
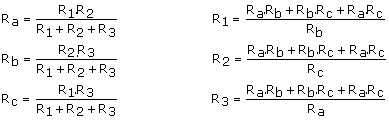
![]() DeltaY
(obtención de las fórmulas, conversión D-Y, conversión Y-D)
DeltaY
(obtención de las fórmulas, conversión D-Y, conversión Y-D)
Arriba
11. ¿Qué plantean las Leyes de Kirchhoff?
11.1 Ley de Corriente de Kirchhoff (LCK) establece: S I nodos = 0
La LCK plantea que la suma algebraica de las corrientes que entran y salen de un área, sistema o unión (nodo) es cero.
11.2 Ley de Voltaje de Kirchhoff (LVK) establece: S V lazos = 0
La LVK plantea que la suma algebraica de las elevaciones y caídas de voltaje a través de una trayectoria cerrada es cero.
Arriba
12. ¿Cómo se resuelven los circuitos con fuentes múltiples en serie o paralelo?
12.1 Circuitos serie:
12.1.1 Dado un circuito con fuentes de voltaje en serie, según la LVK, éstas se pueden reemplazar por una fuente equivalente de valor igual a la suma de los voltajes individuales (c/u con su signo). La razón para realizar esta conexión es incrementar o disminuir el voltaje total aplicado a un circuito.
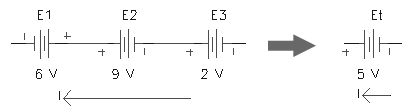
12.1.2 Las fuentes de corriente se conectan en serie, sólo si son de igual magnitud (las direcciones también deben coincidir). La razón para realizar esta conexión es incrementar el voltaje total aplicado a un circuito (y por lo tanto la potencia nominal). Si se colocan en serie dos fuentes de distinto amperaje o de igual valor pero sentido contrario, ambas no funcionarían o se dañarían porque estarían siendo forzadas a trabajar fuera de sus parámetros de diseño.
12.2 Circuitos paralelo:
12.2.1 Dado un circuito con fuentes de corriente en paralelo, según la LCK, éstas se pueden reemplazar por una fuente de corriente equivalente que tenga la magnitud y la dirección de la resultante. La razón para realizar esta conexión es incrementar o disminuir la corriente total que circula por un circuito.

12.2.2 Las fuentes de voltaje se conectan en paralelo, sólo si tienen el mismo voltaje nominal. La razón para realizar esta conexión es para incrementar la corriente nominal (y por lo tanto la potencia nominal). Si se colocan en paralelo dos fuentes de distintos voltajes o iguales pero con polaridades invertidas, ambas no funcionarían o se dañarían porque estarían siendo forzadas a trabajar fuera de sus parámetros de diseño.
Arriba
13. ¿En qué consiste el "análisis de la corriente de rama"?
Consiste en un método para hallar la corriente en cada rama del circuito. Luego, una vez conocidas las "corrientes de ramas", se pueden determinar otras cantidades como el voltaje o la potencia. Pasos a seguir:
- Asignar una corriente distinta con dirección arbitraria a cada rama de la red.
- Indicar la polaridad de cada resistor, como lo determina la dirección de corriente supuesta.
- Si n=nº de nodos esenciales, obtener n-1 ecuaciones aplicando la LCK.
- Si x=nº de corrientes desconocidas, plantear x-(n-1) ecuaciones aplicando la LVK.
- Despejar las incógnitas.
Ejemplo 2:
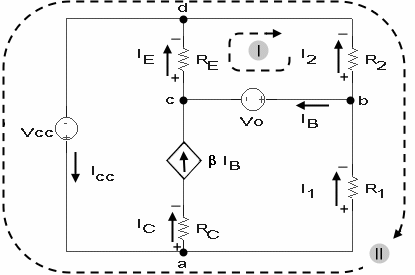
Datos: R1, R2, RC, RE, V0, VCC y b
Las corrientes desconocidas son: i1, i2, iB, iC, iE, e iCC , por lo tanto el sistema mínimo que necesitamos está formado por seis ecuaciones.
-
ver gráfico
-
ver gráfico
-
Planteando la LCK en tres de los cuatro nodos esenciales, obtenemos:
-
Nodo a ® IC + I1 = ICC
-
Nodo b ® I1 = I2 + IB
-
Nodo c ® IE = IB + IC
-
-
No podemos aplicar la LVK a 6-(4-1) = 3 lazos, porque sólo existen dos lazos (I y II en el gráfico) donde no involucramos la caída de tensión en la fuente dependiente. Tomar un lazo diferente, implica agregar otra incógnita.
-
lazo I ® - IE .RE + I2 .R2 - V0 = 0
-
lazo II ® - VCC + I2 .R2 + I1 .R1 = 0
-
Finalmente, la ley de control de la fuente dependiente nos da la sexta ecuación:
IC = b IB
Arriba
14. ¿En qué consiste la técnica de "reducir y regresar"?
Consiste en calcular la resistencia total y la corriente resultante de la fuente, para luego regresar por el circuito hasta obtener la corriente o el voltaje deseados (empleando por ejemplo la expresión del divisor de corriente si se trata de una red en escalera).
Arriba
15. ¿Cómo se obtiene la expresión del divisor de corriente?
Dado el siguiente circuito:
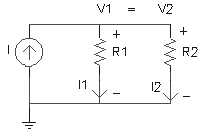
Aplicando la LVK a la malla derecha:
V1= V2 ; aplicando la Ley de Ohm
I1.R1 = I2.R2 (1)
Aplicando la LCK al nodo superior:
I = I1 + I2 ; es decir que: I1 = I - I2 ; y reemplazando esta expresión en (1)
(I - I2).R1 = I2.R2 ; aplicando propiedad distributiva
I.R1 - I2.R1 = I2.R2 ; despejando I2
I2 = I. R1 / (R1 + R2) ; y análogamente para I1
I1 = I. R2 / (R1 + R2)
Arriba
16. ¿Cómo se obtiene la expresión del divisor de voltaje?
Dado el siguiente circuito:
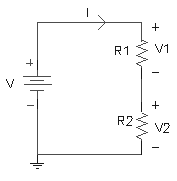
Como la corriente que circula por ambos elementos es la misma:
I1 = I2 = I
Aplicando la LVK al circuito:
V = V1 + V2 (1)
De la ley de Ohm:
V1 = I .R1
V2 = I .R2
Reemplazando las últimas expresiones en (1):
V = I .R1+ I .R2 ; y despejando I
I = V / (R1 + R2)
Ahora, como conocemos la corriente I, podemos calcular la tensión en cada resistor:
V1 = V . R1 / (R1 + R2) ; y análogamente para V2
V2 = V . R2 / (R1 + R2)
Anexo: implementación del divisor de tensión con un potenciómetro
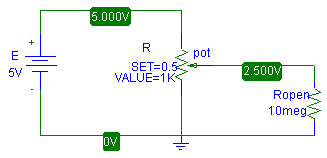
Arriba
17. ¿A qué se denominan puentes de medida?
Generalmente suele denominarse puente a un circuito con cuatro ramas formando un lazo, si sobre dos nodos opuestos se aplica una tensión continua o alterna y sobre los otros dos nodos opuestos se obtiene la salida.
Si se mide la corriente que circula entre los terminales de salida, la configuración se denomina puente de medida. Un puente de medida muy conocido es el Puente de Wheatstone, cuyas ramas son resistivas puras.
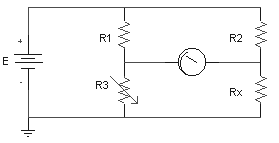
Aplicación: se puede conocer el valor del resistor desconocido (Rx) ajustando el valor de R3 hasta que el indicador de corriente marque cero. Aplicando las leyes de Kirchhoff se puede desmostrar que:
![]()
Estos puentes sirven para medir resistencias de valores intermedios (entre 1ohm y 1Mohm) con una precisión del orden de ±0,1%.
Teoría de Circuitos I - Última modificación: Agosto 5, 2002