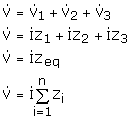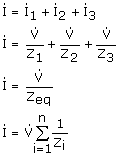8- Análisis Senoidal en Estado Estable
- ¿Por qué es importante el análisis de circuitos alimentados con fuentes sinusoidales?
- ¿Cómo se comportan las fuentes sinusoidales?
- ¿Cómo se calculan los valores eficaces?
- ¿Cómo es la respuesta de un circuito excitado por una fuente sinusoidal?
- ¿Qué es un fasor?
- ¿En qué consisten la transformación fasorial y la transformación fasorial inversa?
- Resumen de números complejos.
- ¿Cómo es la relación V-I para los elementos pasivos?
- ¿Qué es la impedancia?¿Y la admitancia?
- ¿Cómo se analizan los circuitos en la representación fasorial?
- ¿Cómo se combinan las impedancias y las admitancias?
- Conversiones triángulo-estrella y estrella-triángulo
1. ¿Por qué es importante el análisis de circuitos alimentados con fuentes sinusoidales?
De ahora en adelante vamos a analizar el comportamiento de circuitos alimentados con fuentes sinusoidales. Hay dos razones fundamentales para hacerlo:
- es la forma de onda dominante de la industria de potencia eléctrica
- cualquier señal periódica puede representarse mediante suma de sinusoides (Fourier)
![]() Fourier
- contiene ejemplos y ejercicios para desarrollar
Fourier
- contiene ejemplos y ejercicios para desarrollar
Arriba
2. ¿Cómo se comportan las fuentes sinusoidales?
Símbolo de una fuente sinusoidal (tensión o corriente):
![]()
Una fuente de voltaje (corriente) sinusoidal produce un voltaje (corriente) que varía sinusoidalmente con el tiempo.
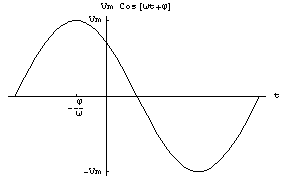
El voltaje sinusoidal se expresa de la siguiente manera:
![]()
donde:
- Vm= amplitud máxima del voltaje sinusoidal
- w = 2pf = frecuencia angular en rad/s
- T = 1 / f = periodo (tiempo en que la función completa un ciclo)
- j = ángulo de fase (determina el valor de la función en t=0)
Observaciones:
-
Cualquier función de variación sinusoidal puede expresarse tanto a través de la función seno como de la función coseno. La cátedra optó por trabajar con la función coseno.
-
Identidades útiles:
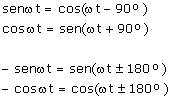
- wt se expresa en radianes pero es muy común expresar j en grados
- si j es positivo, la función se desplaza hacia la izquierda y si j es negativo se desplaza hacia la derecha
Arriba
3. ¿Cómo se calculan los valores eficaces o rms?
El valor eficaz o efectivo o valor cuadrático medio (rms por sus siglas en inglés: root mean square) es el valor de continua equivalente de una señal alterna que entrega la misma potencia promedio que ésta.
El valor rms para toda señal (tensión o corriente), se encuentra determinando:
1- el cuadrado de la señal;
2- el valor promedio o medio de 1); y finalmente
3- extrayendo la raíz cuadrada de 2), es decir:
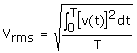
Deducción de la fórmula para Irms:
Si el valor de la corriente eficaz (Irms) es igual al valor de la corriente continua capaz de transmitir a la carga la misma potencia promedio que transmite la corriente alterna.
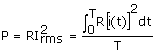
despejando:
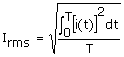
se obtiene la expresión que se esperaba. Resta reemplazar la expresión i(t) y resolver.
Observación:
- Para tensiones o corrientes sinusoidales, se puede demostrar que el valor rms de una señal se obtiene al dividir el valor de la amplitud máxima por raíz de dos.
![]()
Ejemplo 1:
Supongamos un resistor por el cual circula una corriente sinusoidal de valor máximo=14.14A, y que disipa una cantidad de potencia P. El valor eficaz de la corriente alterna es Im/Ö2 = 10A Esto significa que se necesita una corriente continua de 10A para proporcionar la misma potencia P al resistor que la que suministra la corriente sinusoidal de Vm=14.14A.
![]() Valor
medio y rms - contiene ejemplos y ejercicios
para desarrollar
Valor
medio y rms - contiene ejemplos y ejercicios
para desarrollar
Arriba
4. ¿Cómo es la respuesta de un circuito excitado por una fuente sinusoidal?
Supongamos un circuito serie RL excitado por una fuente de voltaje sinusoidal.
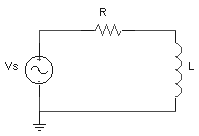
Aplicando LVK obtenemos:
![]()
cuya solución para i(t) es:
![]()
La solución consta de dos términos:
- el primero se conoce como término transitorio: se hace infinitesimal al transcurrir el tiempo
- el segundo se denomina componente en estado estacionario y es el que nos interesa conocer
Observaciones:
- q es el ángulo cuya tangente es wL/R.
- la solución en estado estacionario es una función sinusoidal.
- la frecuencia de la respuesta de un circuito lineal es idéntica a la frecuencia de la señal fuente.
- la amplitud máxima de la respuesta difiere de la amplitud máxima de la fuente.
- generalmente (salvo en los circuitos resistivos puros), el ángulo de fase de la respuesta difiere del ángulo de fase de la fuente.
Ejemplo 2:
Si w=100; R=1; L=20mH; y j=0:
i(t)=-0.2 e-50t + 0.447214 Cos[1.10715-100t]
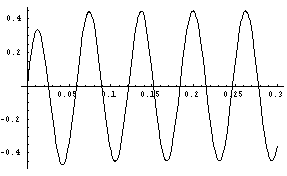
En la anterior figura se observa i(t) en función de la suma de los efectos del término transitorio y de la componente de estado estacionario. La constante de tiempo del circuito es 0.02s, entonces para t = 5t = 0.1s el efecto del término transitorio se puede despreciar y se dice que el circuito ha alcanzado el estado estacionario.
Si se grafican los términos por separado:
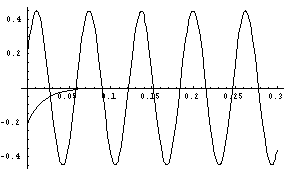
Observación:
-
la representación y manejo de estas formas de onda se simplifica empleando la representación fasorial.
5. ¿Qué es un fasor?
Un fasor es un número complejo con información sobre el valor máximo y la fase de una función sinusoidal.
![]()
Animación: se puede observar la generación de las funciones sinusoidales sen(wt) ycos(wt) para 0£wt£2p a partir de las proyecciones de la función e jwt . Recordar:
![]()
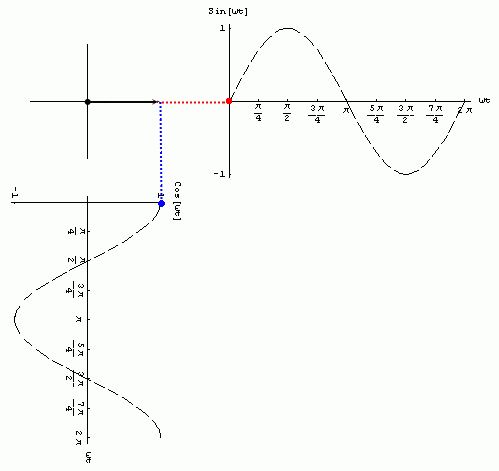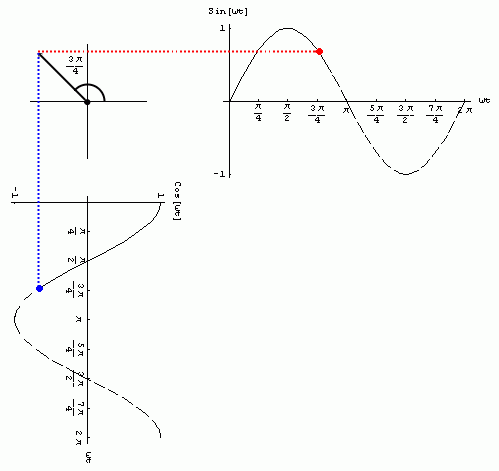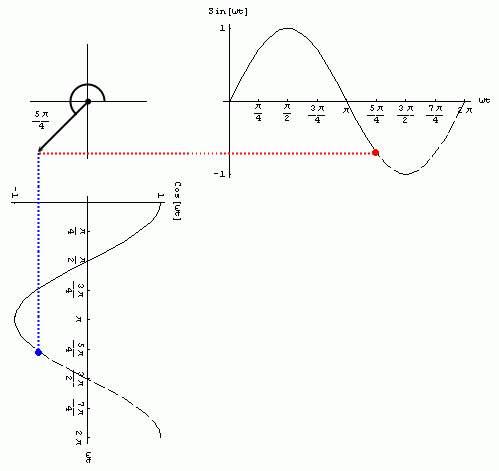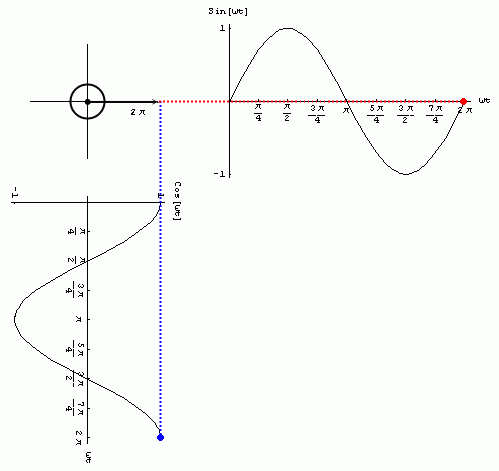
Observaciones:
- el método de los fasores permite obtener de manera sencilla la respuesta en estado estacionario de circuitos excitados por fuentes sinusoidales.
- pueden emplearse las mismas técnicas empleadas para la resolución de circuitos en el dominio temporal.
- si el circuito presenta fuentes con distintas frecuencias, debe emplearse el teorema de superposición.
- el pasaje de un dominio a otro se realiza a través de la transformada fasorial y de la transformada fasorial inversa.
Arriba
6. ¿En qué consisten la transformación fasorial y la transformación fasorial inversa?
La transformación fasorial P{} consiste en pasar de una función temporal a un número complejo que contiene la información sobre su amplitud y fase. Partiendo de la identidad de Euler:
![]()
Cuando se trabaja con circuitos donde todas las fuentes tienen la misma frecuencia, el factor ejwt se omite porque es común a todos los términos de las ecuaciones obtenidas a partir del análisis de circuitos. Entonces:
![]()
Para abreviar se emplea la notación angular:
![]()
La transformación fasorial inversa P -1{} permite obtener la expresión en el dominio del tiempo a partir de la expresión fasorial.
![]()
Arriba
7. Resumen de números complejos.
Para trabajar con fasores tenemos que tener presente la teoría sobre números complejos:
- Un número complejo representa un vector en un plano de dos dimensiones.
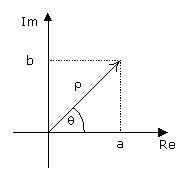
- En el plano complejo, el eje horizontal se denomina Real (Re), y el vertical Imaginario (Im).
- Existen varias maneras de representar un número complejo:

- La transformación de la forma rectangular a polar es:
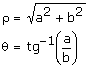
- La transformación de la forma polar a rectangular es:
![]()
- Para sumar y restar números complejos conviene trabajar con la forma rectangular
![]()
- Para multiplicar y dividir números complejos conviene trabajar con la forma polar.
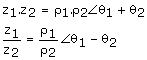
- Hasta las calculadoras científicas mas elementales poseen funciones (generalmente como subfunción de otra tecla) que permiten realizar transformaciones de coordenadas: de rectangular a polar R®P y de polar a rectangular P®R.
Observación:
Arriba
8. ¿Cómo es la relación V-I para los elementos pasivos?
Relación V-I para un resistor
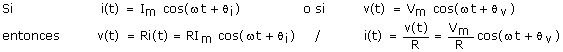
y la transformada fasorial será:

Observaciones:
- Se cumple la ley de Ohm
- i(t) y v(t) representan las ecuaciones en forma temporal de corriente y voltaje
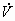 e
e 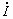 representan los fasores de voltaje y corriente.
representan los fasores de voltaje y corriente.- la tensión y la corriente en un circuito resistivo puro se encuentran en fase.
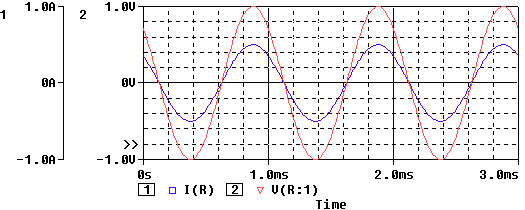
Ejemplo 3:
v(t)=1 Cos (1000 t + 45°) o V = 1 Ð 45°
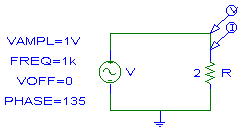
Nota: PSpice trabaja con funciones senoidales. La fase de 135° se debe a que cos(wt+45°) = sen(wt+45°+90°)
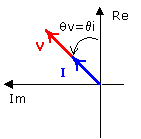
A continuación se observa la representación fasorial y temporal de la corriente y el voltaje sobre el resistor:
|
|
Como se trata de funciones cosenoidales, corresponden a la proyección de los fasores sobre el eje Real. Nota: Para mayor claridad se ha rotado la representación del plano complejo.
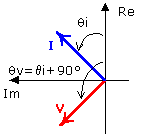
Relación V-I para un inductor

y la transformación fasorial será:
![]()
Observaciones:
- el producto wL se denomina reactancia inductiva (XL) y su unidad es el ohm.
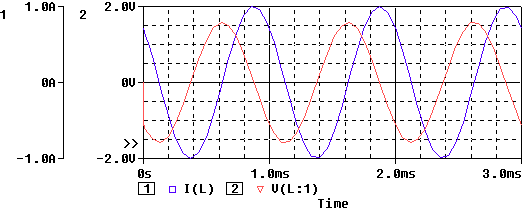
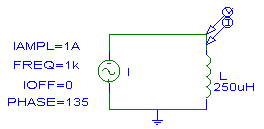
- la tensión y la corriente en un circuito inductivo puro se encuentran desfasadas 90º. Se dice que el voltaje adelanta a la corriente (o que la corriente atrasa al voltaje). Por ejemplo, en el gráfico se observa que la tensión llega a su valor máximo exactamente 90º antes de que lo haga la corriente.
Ejemplo 4:
i(t)=1 Cos (1000 t + 45°) o I = 1 Ð 45°
|
|
|
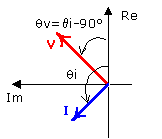
Relación V-I para un capacitor
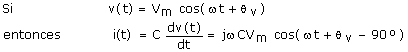
y la transformación fasorial será:
![]()
Observaciones:
- el producto -1/wC se denomina reactancia capacitiva (XC)y su unidad es el ohm.
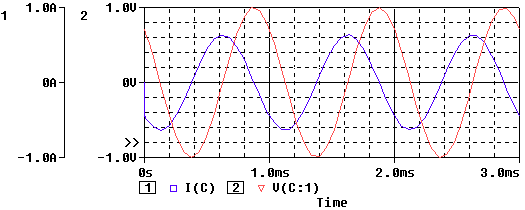
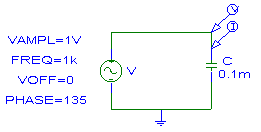
- la tensión y la corriente en un circuito capacitivo puro se encuentran desfasadas 90º. Se dice que el voltaje atrasa a la corriente (o que la corriente adelanta al voltaje). Por ejemplo, en el gráfico se observa que la tensión llega a su valor máximo exactamente 90º después de que lo hace la corriente.
Ejemplo 5:
v(t)=1 Cos (1000 t + 45°) o V = 1 Ð 45°
|
|
|
Arriba
9. ¿Qué es la impedancia?¿Y la admitancia?
Si se comparan las relaciones V-I para los elementos pasivos, se observa que tienen la siguiente forma:
![]()
donde Z representa la impedancia del elemento del circuito. La impedancia de una resistencia es R, la de un inductor es jwL = jXL y la impedancia de un capacitor es 1/jwC = -j/wC = jXC. Para un circuito con múltiples elementos en serie y paralelo, se puede calcular una impedancia equivalente Z=R+jX.
Al recíproco de la impedancia se lo denomina admitancia (Y= 1/Z) y su unidad es el siemens.
Ejemplo 6:
Si Z = 2W - j6W ; la admitancia se calcula como:
![]()
¡Cuidado! No es correcto realizarlo de la siguiente manera:
![]()
A su vez al recíproco de la resistencia se lo denomina conductancia (G=1/R) y al recíproco de la reactancia se lo denomina susceptancia (B=1/X).
Observaciones:
- Si bien la impedancia y la admitancia son números complejos, no son fasores, porque los fasores son representaciones de funciones sinusoidales que varían en el tiempo mientras que Z e Y son consideradas constantes temporales.
- Para reemplazar un circuito por su equivalente en la representación fasorial, se debe calcular la impedancia de cada elemento que compone dicho circuito.
Arriba
10. ¿Cómo se analizan los circuitos en la representación fasorial?
A partir de la expresión de la Ley de Ohm en forma fasorial:
![]()
y de las Leyes de Kirchhoff de las tensiones y corrientes, también en forma fasorial:
![]()
pueden aplicarse todas las técnicas y herramientas desarrolladas para analizar circuitos resistivos en continua, es decir:
- simplificaciones serie-paralelo
- transformaciones D -U
- transformaciones de fuentes
- circuitos equivalentes de Thévenin y Norton
- superposición
- MTN
- MCM
(A modo de ejemplo sólo se desarrollarán los dos primeros ítems.)
Observación:
- El análisis de circuitos en la forma fasorial se reduce a saber cómo construir el circuito equivalente en la representación fasorial y cómo manipular algebraicamente números complejos para poder aplicar las técnicas antes mencionadas.
Arriba
11. ¿Cómo se combinan las impedancias y las admitancias?
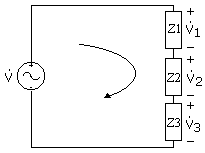
Impedancias en serie:
|
|
|
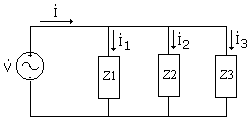
Impedancias en paralelo:
|
|
|
Admitancias:
En paralelo se suman: YT = Y1 + Y2 + Y3 + ........ + Yn
En serie se invierte la suma de sus recíprocos.
Arriba
12. Conversiones triángulo-estrella y estrella-triángulo.
Las ecuaciones de conversión para los circuitos de alterna, se obtienen a partir del mismo desarrollo efectuado para los circuitos de continua.
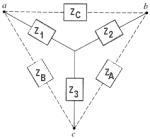
|
Conversión D -U |
Conversión U -D |
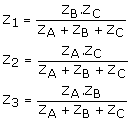
|
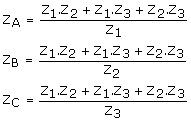
|
![]() DeltaY-Z
(obtención de las fórmulas, conversión D-Y, conversión Y-D)
DeltaY-Z
(obtención de las fórmulas, conversión D-Y, conversión Y-D)
Arriba
Teoría de Circuitos I - Última modificación: Mayo 28, 2002